Valentin Förster and Carl-Alexander Graubner
Valentin Förster, Research Assistant, Institute of Concrete and Masonry Structures, Technische Universität Darmstadt, FranziskaBraun-Straße 3, 64287 Darmstadt, Germany, foerster@massivbau.tudarmstadt.de
Carl-Alexander Graubner, Professor, Institute of Concrete and Masonry Structures, Technische Universität Darmstadt, Franziska-BraunStraße 3, 64287 Darmstadt, Germany, graubner@massivbau.tu-darmstadt.de
ABSTRACT
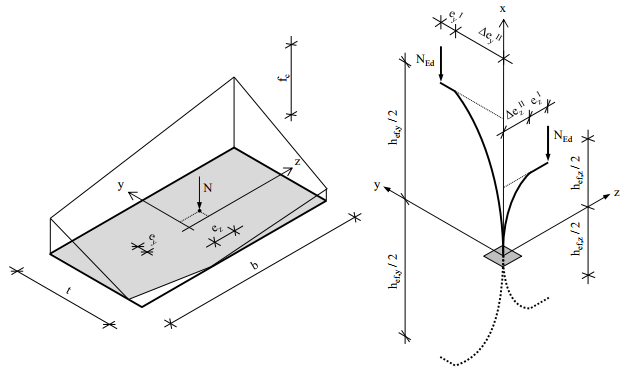
Unreinforced masonry members have to resist vertical loads and bending moments about the weak axis due to rotation of adjacent slabs. If the compression member is part of the bracing system, additional bending moments about the strong axis exist. Thus, the compression member is loaded with a vertical normal force which is eccentric in two ways (out-of-plane and in-plane direction). If the slenderness of the compression member is small, the compression member will fail due to crushing. If the slenderness in one direction is high, the member will fail due to buckling. This research deals with the load carrying capacity of biaxially eccentrically compressed unreinforced masonry walls and columns with linear and non-linear material behaviour. For linear-elastic material, the principles of an analytical model, which considers the geometrical non-linearity and the effect of cracking, is presented. The deflections of the wall can be determined with the derivation of moment-curvature relationships. Thereby, the analytical analysis of compression members considering the effects of 2nd order theory is possible. For a non-linear stress-strain relationship and a limited flexural tensile strength, the evaluation of the load carrying capacity of rectangular cross sections under biaxial bending is complex and has to be performed numerically. In addition to the results of the analytical model, results of numeric calculations are also shown for various eccentricities in both directions.
162